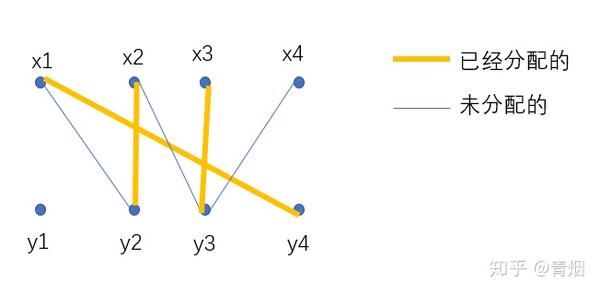
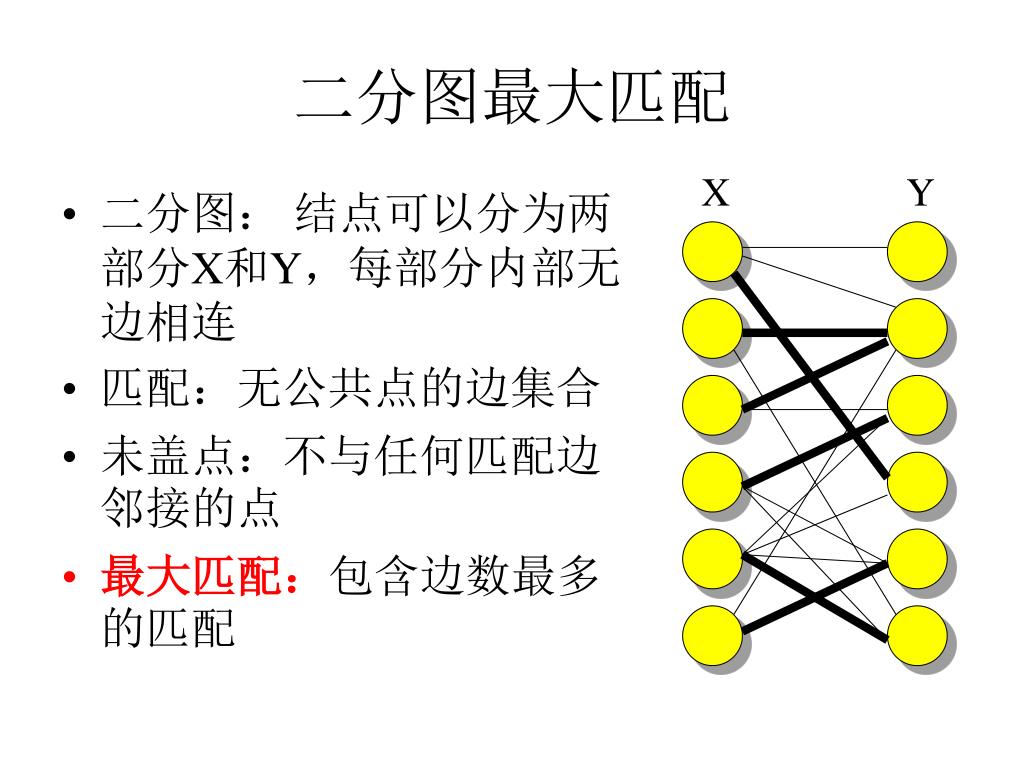
在二分图最大匹配中,每个点(不管是X方点还是Y方点)最多只能和一条匹配边相关联,然而,我们经常遇到这种问题,即二分图匹配中一个点可以和多条匹配边相关联,但有上限,或者说,L i 表示点i最多可以和多少条匹配边相关联。 二分图多重匹配分为二分图多重最大匹配与二分图多重最二分图最大匹配及其应用 二分图与图的匹配 例 1 t he p erfect s tall 题目来源:usaco, poj1274 农夫john的牛棚共有m个牛栏,其中一共 养了n头奶牛。每头奶牛只愿意在它喜欢 的那些牛栏中产奶。一个牛栏只能容纳一 头奶牛,一头奶牛也只在一个牛栏中产奶。 这节课介绍无权二部图中的最大匹配问题 MaximumCardinality Bipartite Matching (MCBM)。匹配 (Matching) 的意思是一些边的集合,这些边不能有共同的节点。MCBM 要求寻找一组满足要求的边,使得边的数量最大化。可以将 MCBM 规约到最大流问题,用 EdmondsKarp 或者 Dinic 等最大流算法求解。
Oi之路 04图论 9二分图 Zory的个人博客
二分图最大权匹配算法
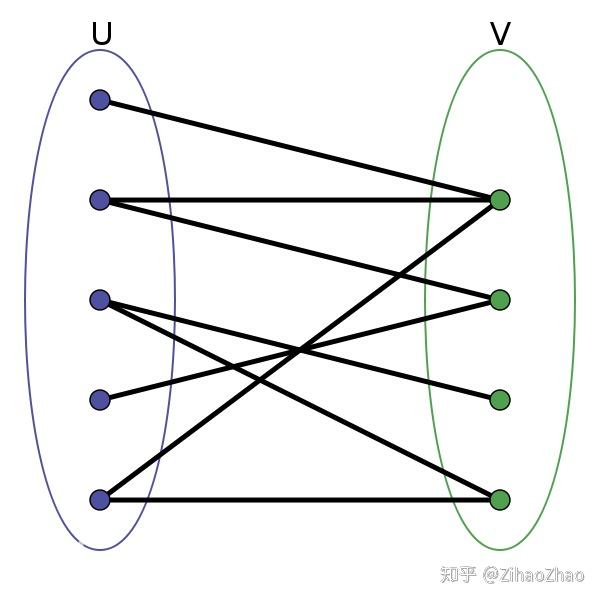
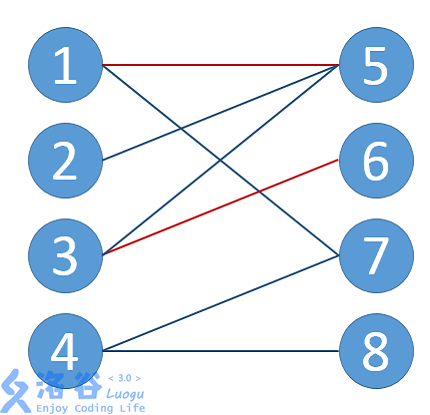
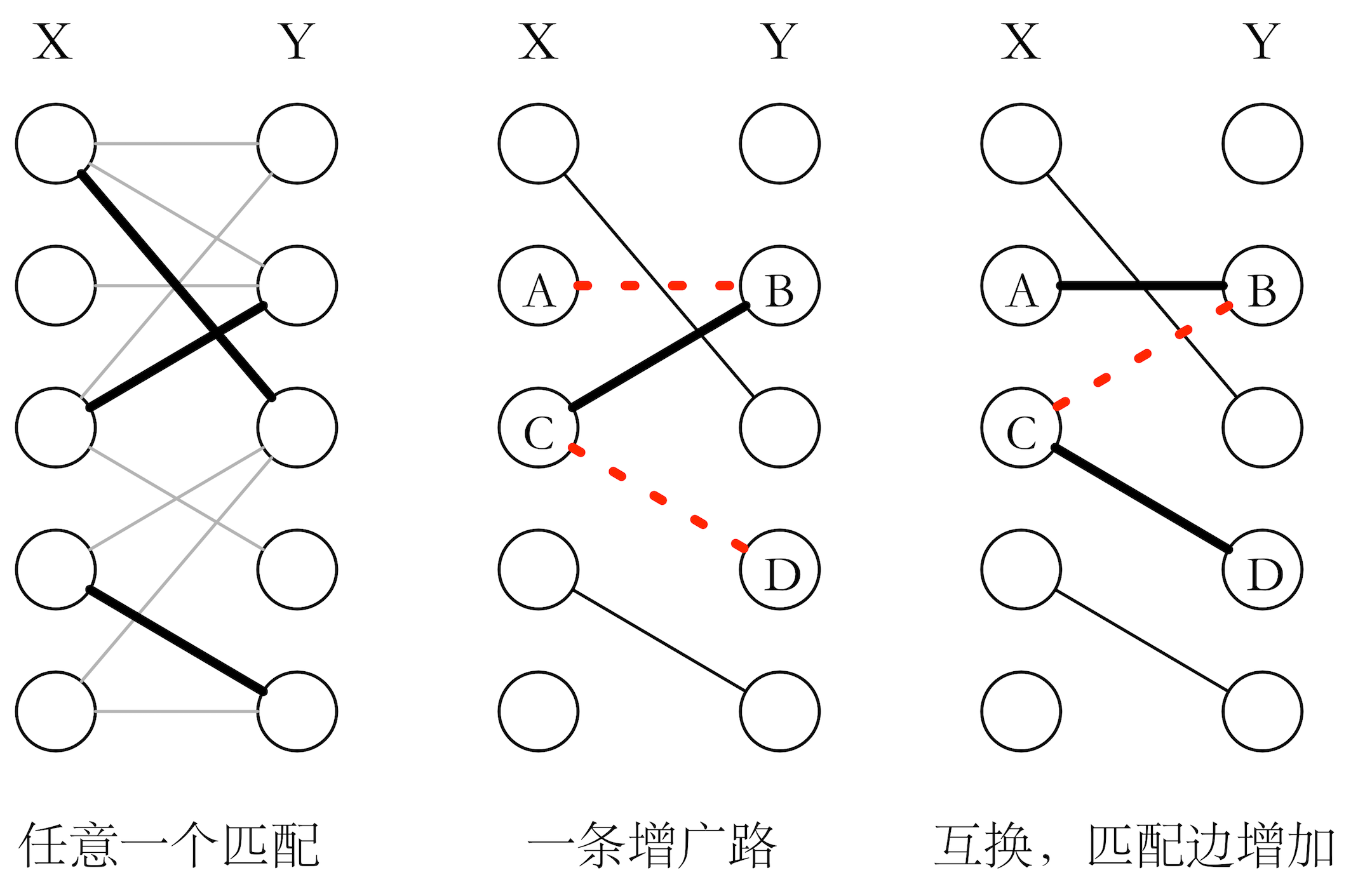
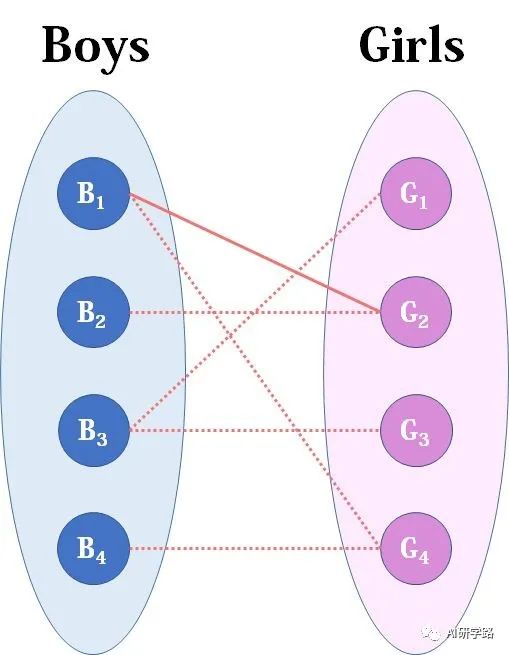
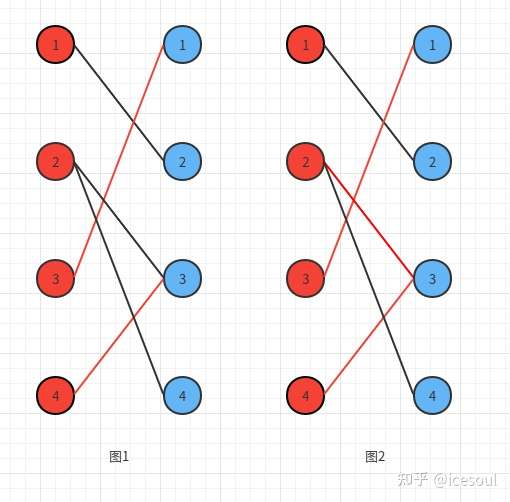
二分图最大权匹配算法-1 二分图最大匹配(boy girl) 2 一般图最大匹配(person person) 3 二分图最大权匹配 4 一般图最大权匹配 三、知识前提——可增广路径 在逐步解决匹配问题的过程中,维护边集M,M在起始时为空,当且仅当存在一条边(i, j)在M中时才称节点i匹配了,这里也说边(i 最大匹配 一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。 图 4 是一个最大匹配,它包含 4 条匹配边。 匈牙利算法解决的问题背景:如果一对男女互有好感,那么你就可以把这一对撮合在一起,现在,你拥有的大概就是下面这样一张




Ytmartian 董家佚 二分图最大权匹配多个解
二分图最大权匹配:KM算法 KM算法用来求二分图最大权完美匹配。 本文没有给出KM算法的原理,只是模拟了一遍算法的过程。 另,博主水平较差,发现问题欢迎指出,谢谢! ! ! ! 现在有N男N女,有些男生和女生之间互相有好感,我们将其好感程度定义为二分图的最大匹配——网络流匈牙利算法_zt在努力程序员秘密 技术标签: 常用模板 匈牙利算法 poj1274 acm 二分图最大匹配 匈牙利算法,时间复杂度n*m;匈牙利算法又称为 KM 算法,可以在 O (n^3) 时间内求出二分图的 最大权完美匹配 。 考虑到二分图中两个集合中的点并不总是相同,为了能应用 KM 算法解决二分图的最大权匹配,需要先作如下处理:将两个集合中点数比较少的补点,使得两边点数相同,再将不
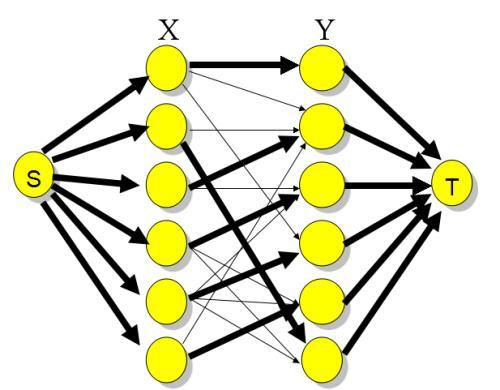
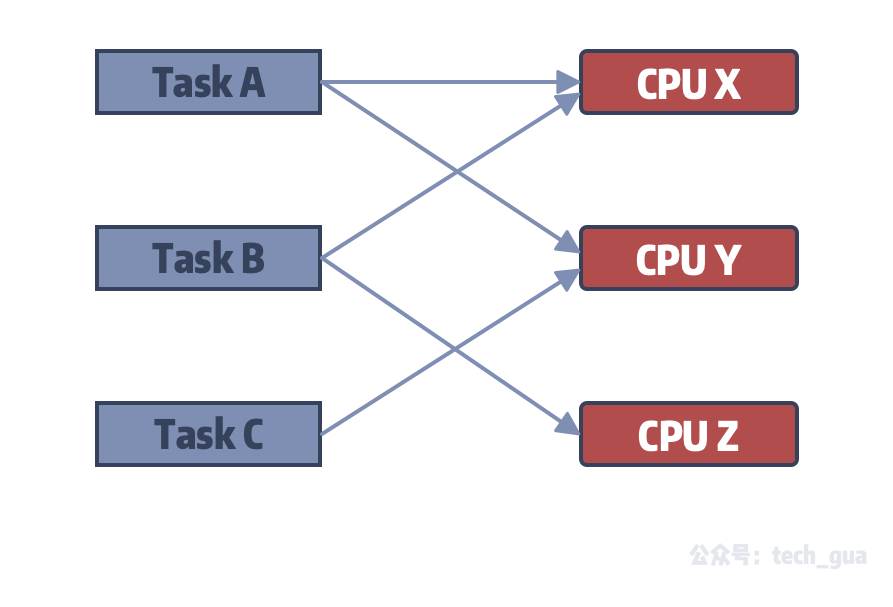
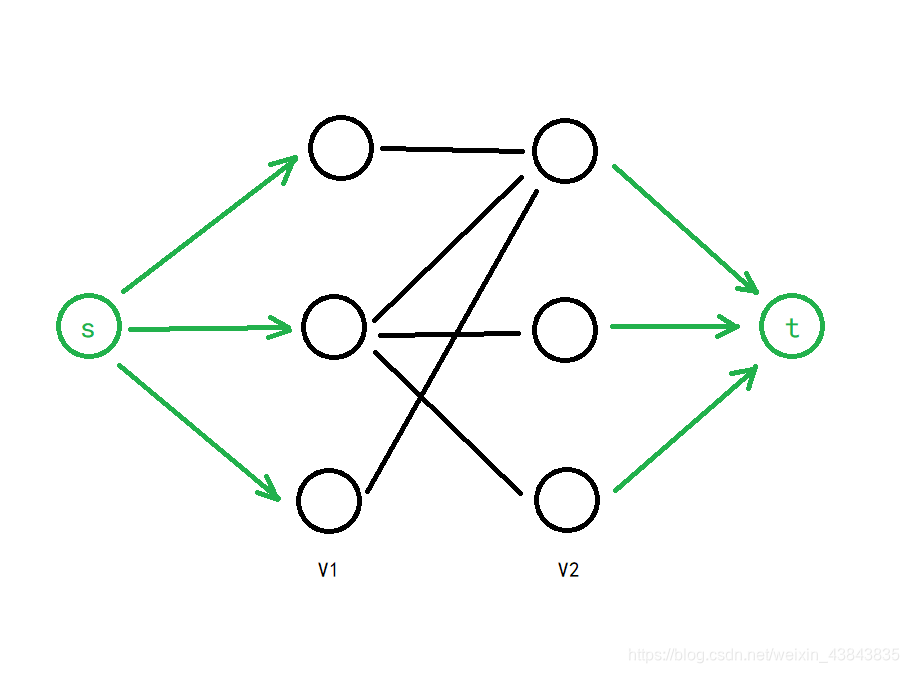
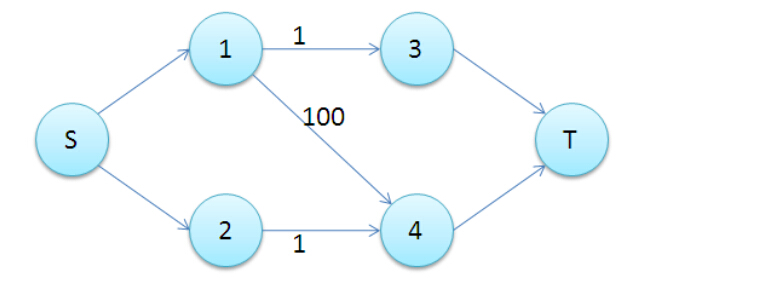
图 4 是一个最大匹配,它包含 4 条匹配边。 匈牙利算法解决的问题背景:如果一对男女互有好感,那么你就可以把这一对撮合在一起,现在,你拥有的大概就是下面这样一张关系图,每一条连线都表示互有好感。 本着救人一命,胜造七级浮屠的原则,你想要尽 在二分图中寻找最大匹配 从本质上来说,二分图匹配其实是最大流的一种特殊情况。 是解决这个问题的关键技巧在于建立一个流网络,其中流对应于匹配,如下图所示。 可以看出,图中添加了源点s和汇点t,它们是不属于V的新顶点。 令已有边的容量为无穷二分图最大匹配可以转换成网络流模型,用Dinic算法求该网络的最大流,可在O()求出。 二分图最大权匹配也可以转换成费用流模型。 限于篇幅,这些不做展开。 二分图最大独立集 选最多的点,满足两两之间
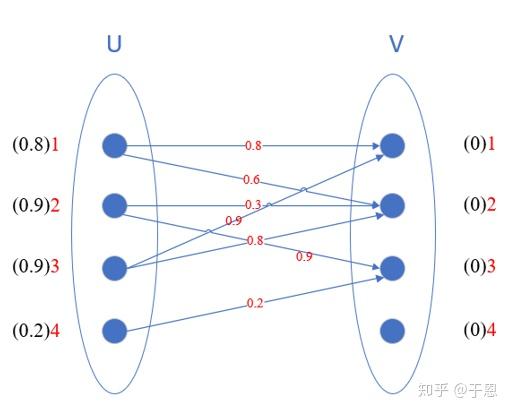
也就是说km算法是来处理有权二分图的。 ☞ 『定义』 KM算法是一种计算机算法,功能是求完备匹配下的最大权匹配。在一个二分图内,左顶点为X,右顶点为Y,现对于每组左右连接XiYj有权wij,求一种匹配使得所有wij的和最大。(copy自百度百科) 二分图带权最大匹配 KM,完备匹配 Posted by elmagnifico on Foreword 前面的二分图,都是基于每条边都是可行的,最大匹配也是只要可行就行,完全不考虑,选择这条边带来的代价,认为所有的边都是代价平等的,然而实际上很多问题不同的选择需要付出KM算法是一种 计算机算法 ,功能是求完备匹配下的最大权 匹配 。 在一个 二分图 内,左顶点为X,右顶点为Y,现对于每组左右连接XiYj有权wij,求一种匹配使得所有wij的和最大。 中文名 KM算法 用 途 求的是完备匹配下的最大权匹配 基本原理 相等子图等 注 意




二分图匹配问题最大匹配以及相关结论 多重匹配 最大带权匹配 带花树算法 Overrate Wsj 博客园



无权二分图的最大匹配求解 匈牙利算法求解 奋斗的程序猿的博客 Csdn博客
30 % 30\% 30% 的数据,满足 n ≤ 100 n\leq 100 n ≤ 100 。 对于 60 % 60\% 60% 的数据,满足 n ≤ 500 n\leq 500 n ≤ 500 ,且保证数据随机 。二分图最大权匹配 二分图的最大权匹配是指二分图中边权和最大的匹配。 KM算法 KM,全名KuhnMunkres,是求解二分图最大权完美匹配的一种算法。 考虑到二分图中两个集合中的点并不总是相同,为了能应用 KM 算法解决二分图的最大权匹配,需要先作如下处理:将两个集合中点数比较少的补给定一个二分图,其左部点的个数为 $n$,右部点的个数为 $m$,边数为 $e$,求其最大匹配的边数。 左部点从 $1$ 至 $n$ 编号



二分匹配的最大流思维 一片瓜田



二分图最大权匹配 Oi Wiki
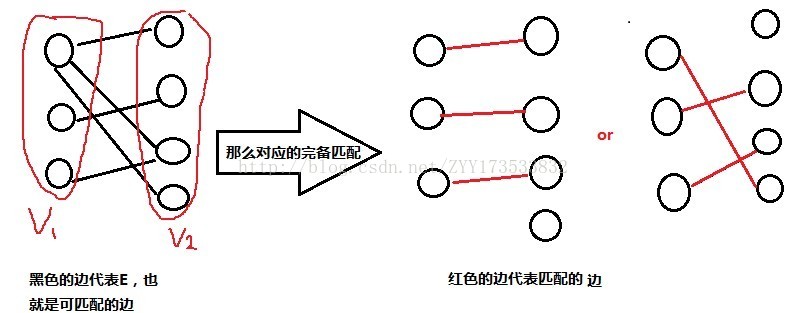
而二分图的最优匹配则一定为完备匹配,在此基础上,才要求匹配的边权值之和最大或最小。二分图的带权匹配与最优匹配不等价,也不互相包含。 我们可以使用km算法实现求二分图的最优匹配。km算法可以实现为o(n^3)。 km的几种转化 km算法是求最大权完备匹配 你好,想请教一下,这个求一般图最大权匹配的算法为什么是正确的呢? 算法大概是这样的: 1从任意匹配开始 2寻找可以通过翻转来增大匹配的路径(环) 3如果找到,则进行增广,并goto 2 4若没找到,则打乱点的顺序(?在二分图的匹配当中,有两种常见的匹配目标,一个是最大匹配,即尽可能多地将 中的点配对;另一个是最佳匹配,最佳匹配的应用场景则是在带权二分图中,最佳匹配就是 中所有的点都与 中的某一个点匹配成对,并且能够使得这些边的权值之和最大的匹配
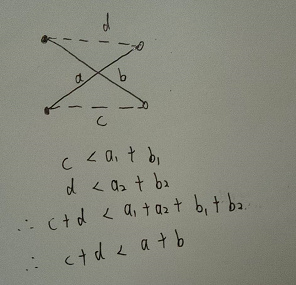



Uvalive 4043 Ants 二分图最大权匹配km算法 H Z Cong 博客园




Learning 二分图最大匹配的konig定理
的权值.左侧带权凸二分图上的最大权值匹配问题 对应着一类经典的调度问题2:给定任务集合和时 间片集合,其中每个任务有释放时间、期限和权值, 且执行时间为单位时间,其调度目标是寻找最大权 值的可行调度任务子集.凸二分图动态匹配问题在 在二分图中,最小覆盖数 等于 最大匹配数,而最大独立数又等于顶点数减去最小覆盖数(=最大匹配数),所以可以利用匈牙利求出最大独立数等等。 a点覆盖集:无向图G的一个点集,使得该图中所有边都至少有一点端点在该集合内。二分图的 带权匹配与最优匹配不等价,也不互相包含 。 以下是一些转换的思路: KM算法是求最大权完备匹配,如果要求最小权完备匹配怎么办? 方法很简单,只需将所有的边权值取其相反数,求最大权完备匹配,匹配的值再取相反数即可。 KM算法的运行




二分图最大权匹配 Maximum Weight Matching In A Bipartite Graph 台部落
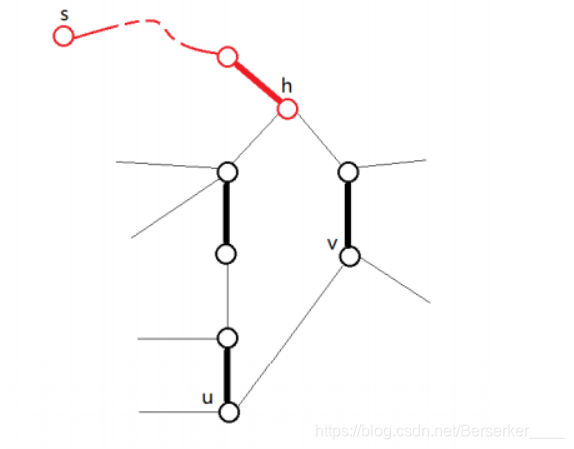



图论 一般图最大匹配 带花树算法 Berserker 的博客 程序员宝宝 程序员宝宝
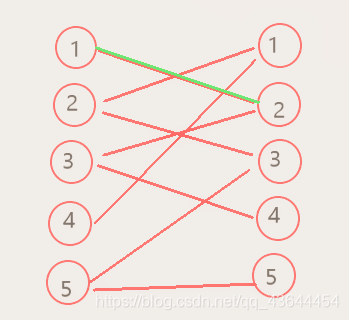
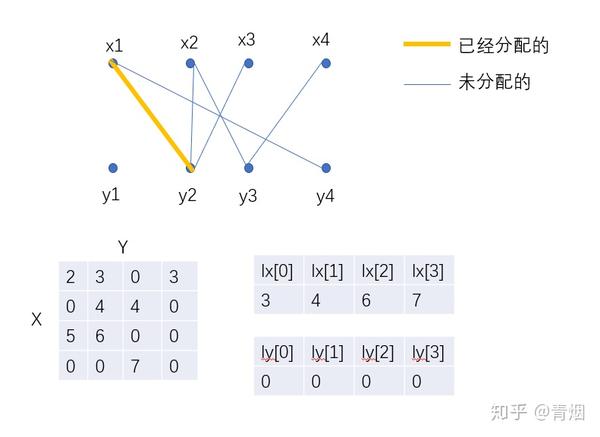
KM算法(二分图的最佳完美匹配) (1)初始化Lx数组为该boy的一条权值最大的出边。 初始化Ly数组为 0。 (2)对于每个boy,用DFS为其找到一个girl对象,顺路记录下S和T集,并更新每个girl的slack值。 若不能为其找到对象,则转3。 (3)找出非T集合的girl的最小 §1图论点、边集和二分图的相关概念和性质 php §2二分图最大匹配求解 html 匈牙利算法、HopcroftKarp算法 node §3二分图最小覆盖集和最大独立集的构造 ios §4二分图最小路径覆盖求解 算法 §5二分图带权最优匹配求解 数据结构 KuhnMunkers算法 闭包 §6小结 less 每章节都详细地讲解了问题介绍,算法原理求解分配问题 (三) 二分图最小权重匹配_wangzhenyang2的博客CSDN博客 在 上一篇文章 中,介绍了二分图的最大匹配问题及其算法,但是分配问题和二分图最大匹配似乎关联不大,为什么要详细介绍二分图最大匹配呢?



图论 二分图匹配基本算法之km算法解析 浅悠悠的个人博客




二部图 二分图 总结 哆啦a瑶的博客 程序员信息网 二分图 程序员信息网
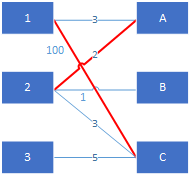
引言 二分图匹配和匈牙利算法(Bipartite Matching and Hungarian Algorithm)在CV领域的后处理算法中是经常可以看到的,比如以下的一些论文: 17年的CVPR工作,OpenPose 利用bipartite matching 来进行,同关节类型的多个人体关键点分配到不同的隶属人体 年的Endtoend Object Detection with 二分图最大权匹配 从前一个和谐的班级,有 n l 个是男生,有 n r 个是女生。 编号分别为 1, , n l 和 1, , n r 。 有若干个这样的条件:第 v 个男生和第 u 个女生愿意结为配偶,且结为配偶后幸福程度为 w 。 请问这个班级里幸福程度之和最大是多少? 二分图最大权完美匹配,表示此时的二分图的边是带有边权的 与二分图最大匹配不同的是,最大权完美匹配侧重于最大权值,要求在保证一个点 最多只能有与其有关系的一条边 被选中的前提下,选出的边的边权总和最大 换做夫妻匹配问题,同样以 一夫一妻制




图论2 江川 Ppt Download




模板 二分图最大权完美匹配km算法
这篇文章讲无权二分图(unweighted bipartite graph)的最大匹配(maximum matching)和完美匹配(perfect matching),以及用于求解匹配的匈牙利算法(Hungarian Algorithm);不讲带权二分图的最佳匹配。 二分图:简单来说,如果图中点可以被分为两组,并且使得所有边都跨越阿里云为您提供二分图最大权匹配 网络流相关的条产品文档内容及常见问题解答内容,还有短信列表模式为对话,8g内存开虚拟机够用吗,lvs dr 不能连接主机,网络故障常见询问问题,等云计算产品文档及常见问题解答。如果您想了解更多云计算产品,就来阿里云帮助文档查看吧,阿里云帮助 赋权二分图最大匹配实验报告docx,赋权二分图最大匹配实验报告 课程设计说明书 设计题目:二分查找程序的实现 专业:班级: 设计人: 山东科技大学年月日 课程设计任务书 学院:信息科学与工程学院专业:班级:姓名: 一、课程设计题目:二分查找程序的实现二、课程设计主要参考资料
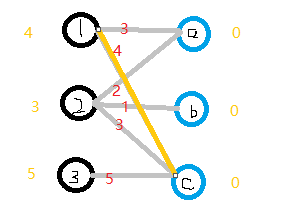



图论 二分图匹配基本算法之km算法解析 浅悠悠的个人博客




二分图匹配 Ppt Download
二分图最大匹配: 给定一个二分图G,在G的一个子图M中,M的边集中的任意两条边都不依附于同一个顶点,则称M是一个匹配。选择这样的边数最大的子集称为图的最大匹配问题(maximal matching problem)。 首先我们先了解两个概念二分图最大权匹配 二分图的最大权匹配是指二分图中边权和最大的匹配。 Hungarian Algorithm(KuhnMunkres Algorithm)¶ 匈牙利算法又称为 KM 算法,可以在 \(O(n^3)\) 时间内求出二分图的 最大权完美匹配。 考虑到二分图中两个集合中的点并不总是相同,为了能应用 KM 算法解决二分图的最大权匹



干货 二分图详解 知乎



算法 日更 第五十期 二分图 Km算法 Debugger Wiki Debugger Wiki




初涉二分图的最大权匹配km算法 自在飞花 Csdn博客




求无权图的最大匹配 匈牙利算法 Winjourn的专栏 程序员资料 程序员资料
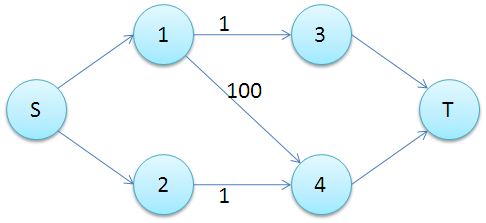



二分图带权匹配km算法与费用流模型建立



蒟蒻图论 二分图最大带权匹配 蒟蒻のblog



带你入门多目标跟踪 三 匈牙利算法 Km算法 知乎



初涉二分图的最大权匹配km算法 掘金




二分图最优匹配 Km算法 简书



二分图判定 二分图匹配 匈牙利算法 多重匹配 最小顶点覆盖 带权二分图匹配 Km算法 Wa的一声就哭了 程序员秘密 程序员秘密



二分图学习记之km算法二分图最大权完美匹配 豌豆ip代理




Ppt 二分图匹配及其应用powerpoint Presentation Free Download Id




Kuhn Munkres算法 二分图最大权匹配 下载 Word模板 爱问共享资料



Km算法原理 证明 梦之泪殇的博客 程序员宝宝 Km算法 程序员宝宝



Oi之路 04图论 9二分图 Zory的个人博客




二分图匹配 匈牙利算法 程序员大本营




0x68 图论 二分图的匹配 码农家园




Km算法 Issue 34 Nhjcacmt Acm Github



二分图最大权匹配km算法 紫芝的博客 Csdn博客 二分图最大权匹配



浅析二分图 最大匹配与最佳匹配 3 Soon 博客园




二分图最大权匹配 Maximum Weight Matching In A Bipartite Graph 台部落



Kuhn Munkres 算法详细解析 Sengxian S Blog




Ppt 二分图匹配及其应用powerpoint Presentation Free Download Id




二分图匹配 搜狗百科



二分图最大匹配 匈牙利算法 洛谷p71座位安排 哔哩哔哩 Bilibili




二分图相关概念及匈牙利算法求解最大匹配 附代码实现 Codeantenna



14 3 有权二部图中的最大匹配maximum Weight Bipartite Matching 哔哩哔哩 Bilibili



Oi之路 04图论 9二分图 Zory的个人博客



二分图匹配 匈牙利算法 知乎




算法导论 之 图 不带权二分图最大匹配 匈牙利算法 的技术博客 51cto博客




二分图相关概念及匈牙利算法求解最大匹配 附代码实现 Codeantenna



Bipartite Matching And Hungarian Algorithm Sen Yang




二分图的最大匹配 完美匹配和匈牙利算法 赏月斋的技术博客 51cto博客



多目标跟踪之数据关联 匈牙利算法 Km算法 知乎



二分图最大权值匹配算法 Km算法 和匈牙利算法 知乎



二分图学习记之km算法二分图最大权完美匹配 豌豆ip代理



简单理解二分图与匈牙利算法 知乎




Java实现二分图的最大权匹配 热爱学习的发呆哥的技术博客 51cto博客




二分图 牛客博客



二分匹配的最大流思维 一片瓜田



二分图 Wikiwand
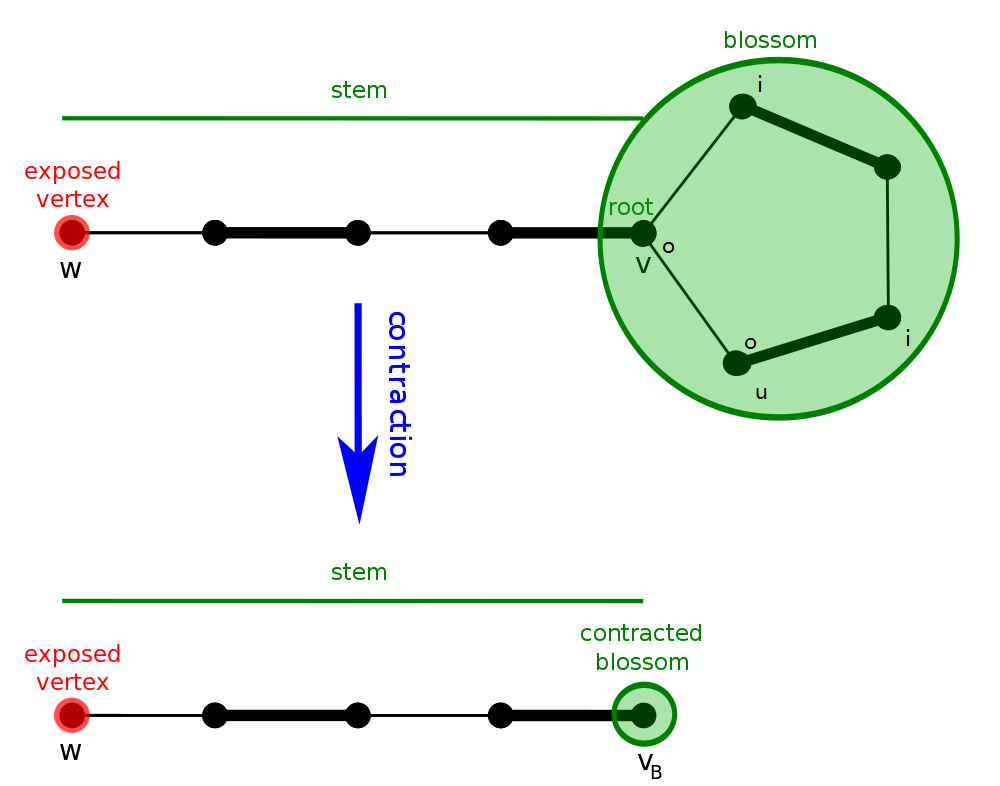



一般图最大匹配 Oi Wiki



Km算法详解 模板 二分图最大权值匹配 Shyoldman的博客 Csdn博客 二分图最大权值匹配




Ytmartian 董家佚 二分图最大权匹配多个解



算法导论 二分图最大匹配 简书



二部图最大权匹配 学习记录二分图匹配问题与匈牙利算法及km算法 三冬评论员的博客 Csdn博客




二分图匹配相关算法及例题分析最大匹配匈牙利算法最大权匹配km算法 二分图类型问题汇总 傻子是小傲娇的博客 大钊 程序员资料



最大二分图匹配 零一人生



图论 最大团问题和最大独立集 二分图相关 上总介的博客 程序员宅基地 团图论 程序员宅基地
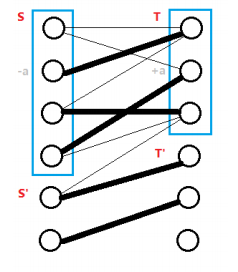



二分图最大权匹配 Oi Wiki



二分图与最大匹配 知乎



二分图最大权值匹配算法 Km算法 和匈牙利算法 知乎




二分图大合集 二分图最大匹配 最小覆盖数 完美匹配以及最优匹配 带权最大匹配 搜索编程资料 就到琅嬛玉洞




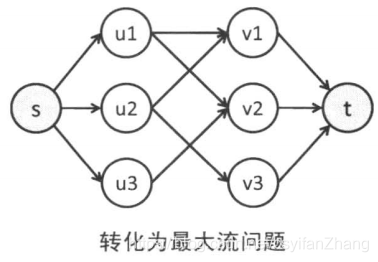
网络流之最大流与二分匹配 二 算法小站




Hdu 34 二分图最大权匹配 牛客博客



算法设计与分析 0016 二分图匹配问题 Gary Chan S Blog



匈牙利算法 二分图最大匹配 Silverblack 程序员资料 程序员资料



二分图带权匹配费用流模型建立 Song Csdn博客



图的匹配 二分图 一般图以及二分图的边覆盖 独立集和顶点覆盖 Csyifanzhang的博客 程序员资料 程序员资料




二分图 2 Sat Discussion 261 Csgrandeur S 1problem1day1ac Github




Uoj 80 二分图最大权匹配 Konjak魔芋 博客园
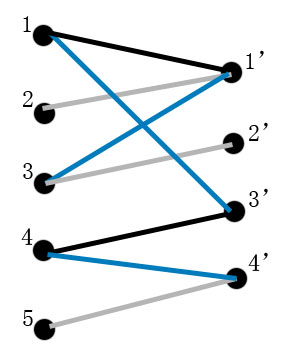



二分图匹配 最大匹配 匈牙利算法 完美匹配 最大权值匹配 Km算法 Weekness的博客 程序员信息网 最大权值匈牙利算法 程序员信息网




二分图的最大匹配 完美匹配和匈牙利算法 赏月斋的技术博客 51cto博客




二分图带权匹配km算法与费用流模型建立
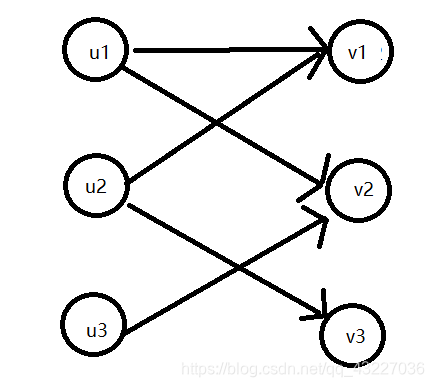



二分图最大匹配 最大流 忆南妄北的博客 程序员信息网 程序员信息网



Ku二分图最大权匹配 Km算法 Hn Doc 360文库



匈牙利匹配和最大权值匹配算法 Silence Cho 博客园




二分图匹配之最佳匹配 Km算法 Lanly 博客园



转载 丘比特的问题 求二分图最大权匹配的算法 转 Feylin Hxf 新浪博客
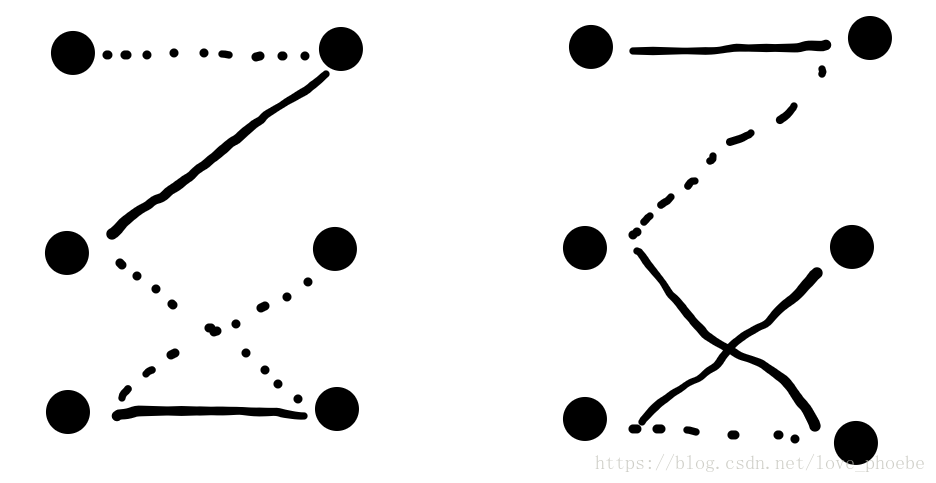



二分图匹配相关算法及例题分析最大匹配匈牙利算法最大权匹配km算法 二分图类型问题汇总 傻子是小傲娇的博客 大钊 程序员资料
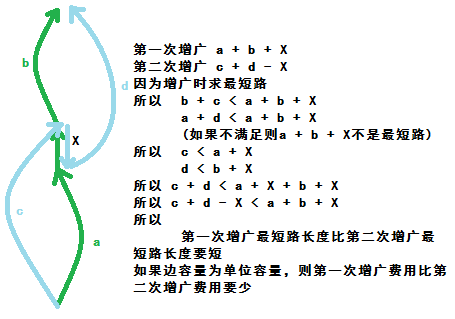



费用流做二分图最大权匹配 我数学不好 Csdn博客



图论 二分图匹配基本算法之km算法解析 浅悠悠的个人博客



算法设计与分析 0016 二分图匹配问题 Gary Chan S Blog




无权二分图的最大匹配求解 匈牙利算法求解 程序员大本营




Km算法原理 证明 布布扣移动版 M Bubuko Com




Ppt 二分图匹配powerpoint Presentation Free Download Id




浅谈算法 二分图匹配 Kyrie Lrving的博客 程序员宝宝 程序员宝宝



二分图与最大匹配 知乎



二分图学习记之km算法二分图最大权完美匹配 豌豆ip代理




算法笔记 二分图最大权匹配 Km算法 Dfs版o N4 Bfs版o N3 繁凡さん的博客 Csdn博客




Ppt 二分图匹配及其应用powerpoint Presentation Free Download Id



Ppt 二分图匹配及其应用powerpoint Presentation Free Download Id




求解分配问题 二 二分图最大匹配算法 Wangzhenyang2的博客 Csdn博客




二分图 网络流初步 Jzp 的博客 洛谷博客
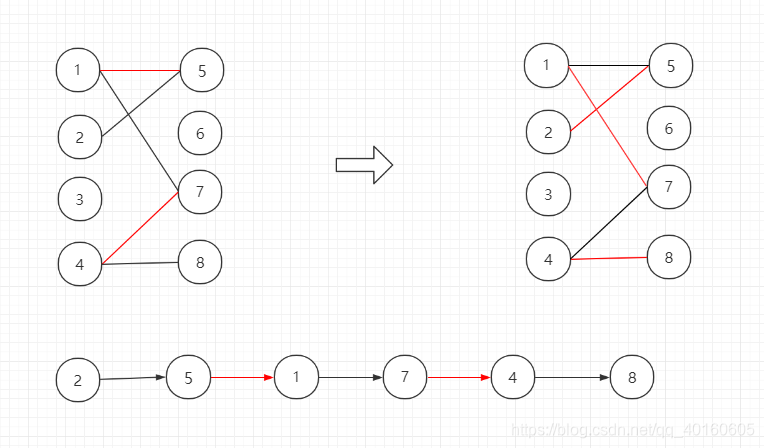



二分图 Brandong 程序员宝宝 程序员宝宝
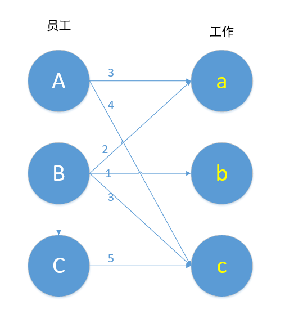



带权二分图匹配 Km算法 Ogmx的博客 Csdn博客 带权二分图



0 件のコメント:
コメントを投稿